Impossible classifications

How descriptive set theory helps us identify unsolvable problems

For the Italian readers: ho aperto un account Instagram in cui mi occupo di temi simili a quelli di questa newsletter. Lo potete trovare qui.

How hard is telling two things apart?

Mathematics is full of objects that seem quite different, yet end up being exactly the same — at least once we wear special glasses that only see certain features of these objects. The more complicated our structures become, the more complicated it might get to determine whether they are actually the same or not — i.e., if there is an isomorphism between them or not. Sometimes an entire career is spent on trying to prove the existence of an isomorphism between some objects; often, famous conjectures can be stated as “these two weird trinkets were actually the same all along”. This unusual form of equality sits at the very core of what mathematicians do and think about every day.

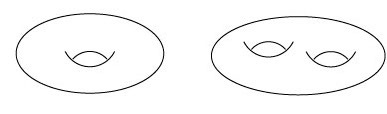
One way of telling two things apart is finding a property that is not shared by them; some kind of crucial difference, one might even call it experimental evidence, proving that the two objects are different. If we are lucky, this evidence comes in the shape of a number. Think of these two surfaces:

If you are a topologist, then you know how to tell them apart — one has one hole, the other one has two. Any isomorphism in this context will preserve this number, so it is a unique invariant of the surface. It is called the genus, and (under some assumptions) it completely classifies these surfaces — in other words, two such surfaces are the same precisely when they have the same genus.

This is perhaps the best example of an invariant: it is a simple number, that can be computed in some way or another, and it completely distinguishes the objects; if I give you a surface of genus 17 and one of genus 275, you can tell me that they are different.

Invariants are one of the most common themes in mathematics, and they pop up every time somebody gets interested in classifying objects, which usually means “understand which other objects they are isomorphic to, and which ones they aren’t”. In a way, it is the most natural question: how unique is this object? Which ones of its defining features characterize it, in the same way that genus does for certain surfaces?

Isolating identifying features that completely classify things is no modern task, and from its very long history comes a cautionary tale: when Plato defined a man as featherless biped, Diogenes brought a featherless chicken into the Academy and declared: “Behold! I’ve brought you a man!”. Sometimes, classification is an unreasonable expectation, invariants don’t exist and the zoo of objects we are dealing with is simply too hard to divide into intelligible categories.

This theme — of extraordinary difficulty — runs throughout a subset (pun not intended) of set theory known as invariant descriptive set theory. Historically, descriptive set theorists have been interested in describing how complicated subsets of the real line can look like; they have built an entire hierarchy, using topological features — how many open sets do I need to intersect to obtain my set? How many closed sets do I need to take a union of? How many times do I need to project “simple” sets to obtain a complicated set? Among these complexities, we think of Borel sets as being relatively simple: these are the sets obtained from open sets by taking countable unions, countable intersections and complements. In a way, a Borel set can be reconstructed from open sets (think of intervals of the real line) together with countable information.

This hierarchy seems a tempting gauge for measuring other complexities. Back to our original problem, we can consider a set X of objects to be classified, together with an equivalence relation E on X that tells us up to what we’d like to classify these objects. For example, X might be the set of the surfaces that we have discussed, and E might be the relation of homeomorphism. If X is a nice enough topological space, one can apply the descriptive set theoretical perspective and ask: is E a Borel subset of X×X? If yes, then maybe invariants exist; otherwise, it seems very unlikely that a decent classification will ever be available, considering that E itself is incredibly complicated. Showing that certain equivalence relations are not Borel is typically referred to as anti-classification — if invariants exist, they must be absurdly complicated.

Many classification problems are not Borel, so are regarded as unsolvable — for example, the isomorphism between countable graphs is not Borel. Invariants that distinguish countable graphs, if they even exist, have to be very hard to imagine, almost impossible. Proving this requires us to turn the classification problem — a priori just a question about isomorphisms between some combinatorial objects — into a topological one. To do so, we must encode countable graphs in a shape, a topological space that remembers the original data.

What is a countable graph? It is the choice of a subset

\(V \subseteq \mathbb N^2\)

that encodes the edge relation: two natural numbers n and m are connected by an edge precisely when (n,m) is in V. Thus V completely determines the graph.

Now V can be seen as a point in a topological space, namely the space

\(V \in 2^{\mathbb N^2}\)

which descriptive set theorists love very much. It can be seen as an infinite product of copies of 2, which then receives the product topology. While a bit counterintuitive at first, it is in fact quite a nicely behaved space, for which the notion of “Borel” makes sense. Then one can look at the relation E defined on this space by “E(V,W) holds precisely when the graphs encoded by V and W are isomorphic”. The theorem that can be proved is that E is not Borel, so it is quite complicated.

The object “infinite product of copies of 2” is a useful encoding of seemingly abstract and complicated objects, like generic countable graphs. Its topological properties, then, can be used to study the shape of the isomorphism relation, producing concrete and sometimes surprising results on classification. This is, however, not a failproof technique; in the case of geometrical objects like the surfaces at the beginning, it is not quite clear what kind of topological space should be used to study classifiability. In an ironic twist of events, there seems to be no clear concept of what the shape of shapes should be (that is, unless the words moduli space enter the picture, which would open a whole another chapter of this story).